Vacation Scholarships Projects

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Algebra

Understanding the Riemann zeta function

Can we make sense of the divergent series 1^s+2^s+3^s+… when s>=1? This project studies the Riemann zeta function using modular forms.

Contact: Chenyan Wu chenyan.wu@unimelb.edu.au

Structure in space: aperiodic tiling

We can tile a plane using squares for example. The pattern repeats itself. This project considers ways of tiling the plane without repetition using number theory and representation theory.

Contact: Chenyan Wu chenyan.wu@unimelb.edu.au

Multipartitions and level-rank duality

Contact: Ting Xue ting.xue@unimelb.edu.au

Cyclic quivers and distinguished orbits

Contact: Ting Xue ting.xue@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Analysis

There are no specific projects listed. Please get in touch directly with potential supervisors in this area.

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Applied Mathematics

Lava flow through a forest

Recent field studies have identified that vegetation can have a strong effect on the flow of lava as it migrates downslope from a volcanic vent. Forests act as a network of obstacles that can slow and divert the advancing lava. This project will investigate the interaction of shallow viscous flows with arrays of obstructions to determine how their formation influences the flow field and the force exerted. Existing numerical codes are available for the student and the main aim will be to develop simple analytical solutions to describe the flow physics.

Contact: Edward Hinton ehinton@unimelb.edu.au

Autonomous propulsion of nearly spherical nanoparticles trapped in acoustic fields

When asymmetric nanoparticles are trapped at the pressure node/velocity antinode of an acoustic field, they can swim autonomously due to a phenomenon called ‘acoustic streaming’. While this phenomenon has been explained for arbitrary shapes, analytical formulae only exist in the highly idealised cases of a perfect sphere and a two-sphere system. This project aims to develop an analytical formulation for how a nearly spherical particle behaves in an acoustic trap. The project will use asymptotic methods on the Navier-Stokes equations alongside domain perturbations on nearly spherical geometries.

Contact: Jesse Collis jesse.collis@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Discrete Mathematics

Lattice models of polymer systems

Long chain polymers like DNA can be modelled by walks, polygons, trees, and various other combinatorial structures embedded in lattices. This project aims to investigate new polymer models. This can be approached using exact solution techniques or computational methods like series enumeration and random sampling.

Contact: Nick Beaton nrbeaton@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Geometry and Topology

Asymptotic properties of random knots

Knotted structures are ubiquitous in nature and of interest in many areas of pure and applied mathematics. There are several different ways of representing a knot, each with its own advantages and drawbacks. In this project, we will investigate large scale properties of random knots and how these change according to the model used. Time permitting, we will discuss applications to biology and biophysics.

Contact: Daniele Celoria daniele.celoria@unimelb.edu.au (joint with Agnese Barbensi)

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Learning and Teaching Innovation

Case studies for “RealStat”

The teaching resource “RealStat” is a collection of case studies involving statistics and data science.  In all of the projects, the Statistical Consulting Centre at the University of Melbourne was involved, by providing assistance, advice, analysis and support to the researchers.

The case studies have rich material that provides context and background, which typifies the usual presentation of a project to a statistician. This makes them ideal for teaching students about authentic statistical practice, and they have been used in a variety of ways in subjects at undergraduate and postgraduate level.

The vacation scholar project involves working on some new case studies, to add to the current set.

We are seeking a student with a strong background in statistics and good writing skills.  Experience with R and web programming would be beneficial.

Contact: Ian Gordon irg@unimelb.edu.au (jointly with Sue Finch)

Visual blocks to help students learn syntax

Learning mathematical syntax is essential for understanding and communicating mathematics, but it is something students often find hard to master. Maths Blocks (www.mathsblocks.com) is a system of visual blocks intended to help students with mathematical syntax. This project will investigate ways to extend Maths Blocks to support additional areas of mathematics, such as functions and their inverses, sets, or other topics. It will involve some mathematics (such as formal language theory and type theory), some learning theory, some software design, and (potentially) some programming.

Contact: Anthony Morphett a.morphett@unimelb.edu.au

Mathematical modelling of a classroom disease epidemic simulation

The 'Handshake game' is a classroom simulation of an infectious disease outbreak, which can be used in teaching infectious disease modelling. In this project, we will model the progression of the handshake game using ODE (ordinary differential equation) models. In particular, we will investigate how well the classic SIR model describes the progression of the handshake game, and explore variants of the SIR model which may give a better fit. This will involve some mathematical modelling, numerical solving of ODEs, and model fitting using MATLAB, Python or similar software.

Contact: Anthony Morphett a.morphett@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Mathematical Biology

Multicellular Systems Biology

My research is on the interface between applied mathematics numerical methods scientific computing and biology. We use theoretical tools to try to get a better understanding of organ and tissue development and disease.

Due to recent increases in the amount and quality of cell level imaging data, and matching advances in computational power, multicellular modelling has become ever more popular. Multicellular modelling considers cells as discrete entities and represents their interactions using mathematical formalisms, both stochastic and mechanics based. This allows tissues to be simulated, with tissue level behaviour and properties being emergent rather than imposed.

Various projects are available focusing on modelling and on numerical methods. See my website for examples of my work.

Contact: James Osborne jmosborne@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Mathematical Physics

Lattice models of polymer systems

Long chain polymers like DNA can be modelled by walks, polygons, trees, and various other combinatorial structures embedded in lattices. This project aims to investigate new polymer models. This can be approached using exact solution techniques or computational methods like series enumeration and random sampling.

Contact: Nick Beaton nrbeaton@unimelb.edu.au

Symmetric polynomials and vertex operators

Symmetric polynomials with several variables are important objects in physics, they enter into the expression of quantum wave functions, but also into the non-perturbative analysis of certain quantum field theories. Around 1990, Naihuan Jing developed a method to study these symmetric polynomials based on vertex operators, an important tool of 2d conformal field theories (statistical physics, string theory). The goal of this project is to learn Jing's technique and apply it to generalize the family of Hall-Littlewood polynomials. The main references for this project are Jing's 1991 paper "Vertex Operators and Hall-Littlewood symmetric functions" and part of Macdonald's lectures on "Symmetric Functions and Orthogonal Polynomials". A good understanding of basic linear algebra will be essential for this project.

Contact: Jean-Emile Bourgine jean-emile.bourgine@unimelb.edu.au

Individual projects in the areas of field theory, supersymmetry, string theory and the mathematics behind

Contact: Johanna Knapp johanna.knapp@unimelb.edu.au

Quantum groups and integrable lattice models

In this project the student will learn about some algebraic constructions behind solvable physical models.

Contact: Sasha Garbali alexandr.garbali@unimelb.edu.au

Quantum entanglement

In this project, we will study the concept of quantum entanglement, famously coined by Albert Einstein as "spooky action at a distance". The goal is to understand and classify how different parts of a quantum system can be quantum mechanically correlated, which cannot be described by classical physics. The project requires a solid background in linear algebra and will give the opportunity to learn some advanced topics (e.g., in Lie theory and random matrix theory), while no prior physics knowledge is required.

Contact: Lucas Hackl lucas.hackl@unimelb.edu.au

Black hole information paradox

In this project, we will explore the famous black hole information paradox, which asks the question what happens to the information of matter falling into a black hole once the black hole is completely dissolved into thermal Hawking radiation. The goal is to understand the paradox, analyze several potential solutions and attempt to relate them to the concept of quantum entanglement. The project requires a solid background in linear algebra and will give the opportunity to learn some advanced topics (e.g., in differential geometry and Lie theory), while no prior physics knowledge is required.

Contact: Lucas Hackl lucas.hackl@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Operations Research

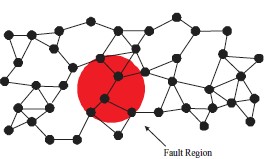
Floods, fires and explosions: how to design survivable networks in the modern age.

Much of society’s critical infrastructure takes the form of large-scale networks. Think of examples such as the power grid, the NBN, gas and water pipelines, and transportation networks. All such networks are potentially vulnerable to natural disasters, or even terrorist attacks. Significant interruption to these networks can wreak havoc. So the question is: how do we design these networks to be robust against local, regional destruction, without blowing the national budget?

In this project we will use planar geometric graph models for this problem and analyse survivability when the destruction region is modelled as a circular disk. In particular, we would like to find algorithms for optimally designing networks that are survivable against failures of a given maximum radius. The project will use mathematical tools from graph theory, optimisation, computer science and just a little bit of Euclidean geometry.

Contact: Charl Ras cjras@unimelb.edu.au

Algorithms for distributed, decentralised optimization

The field of distributed optimisation studies algorithms suited to solving optimisation problems which can exploit computing architectures such as those used in high performance and cluster computing. Within this paradigm, the basic computing model considers a fleet of "simple" devices, connected via some network topology, which work collaboratively to solve a complex problem. Each device has some partial knowledge of the problem, which is private to that particular device, and the ability to do work. This project will study algorithms for solving optimisation problems in distributed, decentralised systems using recent advances in the field of monotone operator splitting.

Contact: Matthew Tam matthew.tam@unimelb.edu.au

Charging Coordination for Plug-in Electric Vehicle Fleets

With an increasing uptake of Plug-in Electric Vehicles (PEVs), it is becoming increasingly important for aggregate charging behaviour to be coordinated in way that does not place undue stress on electricity distribution infrastructure. On the other hand, PEV owners typically make charging decisions based on individual factors (such as minimising electricity costs) rather than factors affecting electricity distribution infrastructure as a whole. To reconcile these competing interests, this project will examine decentralised algorithms based on game theory for making coordinated optimal charging decisions in fleets of non-cooperation PEVs.

Contact: Matthew Tam matthew.tam@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Statistics

Tracking Physical Activity: How reliable is your smart watch?

Physical inactivity has been long associated with elevated risk of various cardiovascular diseases and cancer. Wearable physical activity (PA) trackers such as Fitbit and Xiaomi Smartband provide cost-effective methods for capturing physical activities patterns at high resolution. They are being increasingly used in research settings as intervention as well as providing health- related information to consumers. However, data from these wearable trackers are known to contain systematic biases. For example, these wrist-worn devices are known to overestimate steps for activities involving wrist movement such as folding laundry or playing video game.

In this project, we propose a Hidden Markov Model to improve estimation of physical activity using data from wrist-worn wearable device. The model will use step counts, heart rate and other relevant manifest variables. Models with different emission probability and sojourn time distributions will be compared and the best model will be selected using real datasets from a set of patients recruited as part of a clinical trial at the Baker Institute (https://baker.edu.au/research/clinical-trials/optimise-study). Once developed the best model will be further validated using another set of patients. Simulation studies for assessing the robustness of the model against missing data due to irregular wearing pattern will also be investigated.

Contact: Agus Salim salim.a@unimelb.edu.au, www.salimlab.org

Rank-dependent branching processes

Many animal populations feature a social structure with dominance hierarchy. This is common in monkey populations such as baboons and vervets, as well as in wolves, birds and fishes. In such populations, individuals compete for resources and mating opportunities within their social group; relationships and interactions between the individuals result in a relative rank (social order) being created. An individual’s rank may depend on the rank of their parent or their siblings, as well as their age, experience, and physical fitness; the social rank of individuals is subject to change when a dominant animal (high rank) is challenged by a subordinate one (lower rank) through a conflict. The rank can affect access to food, territory, mates, and even survival. There are benefits and costs to being a dominant individual: those individuals have better foraging and reproductive success, however they suffer from more stress which may lead to a loss of fitness and lower life expectancy. Insights into the behaviour of individuals in these hierarchical societies can lead to better management of threatened and endangered populations.

Inspired by real ecological issues concerning the vervet monkeys, this project aims to model dominance hierarchy in populations using particular multitype branching processes, called rank-dependent branching processes.

Contact: Sophie Hautphenne sophiemh@unimelb.edu.au

Verifying election results using statistical techniques

Once an election result is announced, how confident can we be that it is correct? Were the ballots interpreted correctly and the votes properly counted? Was any of the data manipulated in the process?

There is increasing interest in developing techniques to audit an election result by inspecting a small sample of ballots. Such audits can provide more assurance in the reported election outcome, or possibly cast doubt and lead to a recount. Methods for auditing simple elections have been well established, but are still in development for more complex elections such as the preferential voting systems used in Australia.

This project will involve investigating the properties of different statistical audit methods, via simulations and/or mathematical derivations. Of particular interest is comparing Bayesian and classical approaches.

Contact: Damjan Vukcevic damjan.vukcevic@unimelb.edu.au

Analysis of categorical ratings

A common task in health and medicine is the classification of patient information into one of several categories by a trained expert. This could include assessing the presence and type of a tumour from a medical image or providing a disease diagnosis from a series of medical tests. Often such judgements are hard to make and error prone: two experts may rate the same scenario differently or the same expert may provide alternative ratings of the same scenario when rating it multiple times on different occasions.

This project will involve exploring statistical models for these types of data, using real and/or simulated data. It may include developing new models for specific datasets, implementing the models in software, and benchmarking the performance of different models under a range of scenarios.

Contact: Damjan Vukcevic damjan.vukcevic@unimelb.edu.au

Listed on this page are current research projects being offered for the Vacation Scholarship Program.

For more information on this research group see: Stochastic Processes

Rank-dependent branching processes

Many animal populations feature a social structure with dominance hierarchy. This is common in monkey populations such as baboons and vervets, as well as in wolves, birds and fishes. In such populations, individuals compete for resources and mating opportunities within their social group; relationships and interactions between the individuals result in a relative rank (social order) being created. An individual’s rank may depend on the rank of their parent or their siblings, as well as their age, experience, and physical fitness; the social rank of individuals is subject to change when a dominant animal (high rank) is challenged by a subordinate one (lower rank) through a conflict. The rank can affect access to food, territory, mates, and even survival. There are benefits and costs to being a dominant individual: those individuals have better foraging and reproductive success, however they suffer from more stress which may lead to a loss of fitness and lower life expectancy. Insights into the behaviour of individuals in these hierarchical societies can lead to better management of threatened and endangered populations.

Inspired by real ecological issues concerning the vervet monkeys, this project aims to model dominance hierarchy in populations using particular multitype branching processes, called rank-dependent branching processes.

Contact: Sophie Hautphenne sophiemh@unimelb.edu.au